Influence of Flange on Seismic Performance of 1,100-kV Ultra-High Voltage Transformer Bushing
Chang He,a) Qiang Xie,a) and Yong Zhoua)
Failures of the metal flange were observed in transformer bushings in pre- vious earthquakes. In order to evaluate the influence of the flange on the seismic responses of 1,100-kV ultra-high voltage (UHV) bushing, two types of flanges were selected, which used different materials and layouts. The finite element (FE) and theoretical analyses were first carried out. The results indicate that there is an out-of-plane rocking effect at the flange bottom plate, and the flange will be damaged if the stiffeners are improperly designed. Then two identical bushings using different flanges were tested on the shaking table. The bottom plate of the cast aluminum flange cracked along the stiffeners accompanied by oil leakage. However, the UHV bushing with stainless steel flange survived in the test. It is concluded that the properly designed flange could improve seismic performance of UHV transformer bushings. [DOI: 10.1193/122517EQS266M]
INTRODUCTION
Large power transformers are indispensable equipment in substations, which are impor- tant joints in electrical lifeline systems. If power transformers were destroyed in an earth- quake, there would be huge direct or indirect economic losses, and the electricity interruption would make the disaster relief and rehabilitation very difficult.
During the past decades, earthquakes have severely damaged substations, such as the Kobe earthquake in Japan (Shinozuka et al. 1999). Moreover, in the earthquakes in Mexico (Johnson and Iliev 2012), Chile (Fujisaki et al. 2014), and Haiti (Goodno et al. 2011) in 2010 and the M 9.0 Tohuko earthquake in Japan in 2011 (Eidinger et al. 2012), the overturning and slippage of the transformer tanks were common. Because of the brittleness of the porcelain material, which is used to manufacture the transformer bushings, the porcelain bushings have higher earthquake vulnerability than the transformer tanks. The transformer bushings suffered havoc during the Northridge earthquake in the United States in 1994 (Schiff 1995). In 2007, a nuclear power plant was taken offline due to the damage of a 500-kV transformer bushing destroyed by the Niigata earthquake (Mishima et al. 2008). In the M 8.0 Wenchuan earth- quake, 109 power transformers were damaged, which concentrated on the fracture of the por- celain insulators (Xie et al. 2011). Three typical failures of the transformer bushings were found in the previous earthquakes: (1) the transformer bushing cracked at the bottom cross section; (2) the rubber sealing ring in the flange slipped, and the oil leakage happened; and (3) the metal flanges cracked (Figure 1). Composite transformer bushings are adopted in

Figure 1. Failure of the metal flange of a 220-kV transformer bushing in the Wenchuan earthquake.
substations. The strength of the polymer material is higher than that of the porcelain. However, there are some limitations for the polymer bushings to be widely used in substations due to the consideration of electrical insulation failure.
Theoretical research on the seismic performance of the transformers and their bushings are difficult due to their complex structures. Filiatrault and Matt (2005) experimentally studied the amplification effect of the transformer tank via a mock transformer-bushing system and demonstrated that the transformer tank would amplify the acceleration at the base of the bushing mounted on it. Filiatrault and Matt (2006) also investigated four types of high voltage transformer-bushing systems by FE analyses and discovered that the dynamic amplification factor at the base of the bushing was larger than the recom- mended factor 2.0 in IEEE Std 693-2005 (IEEE 2005) at the fundamental frequency of the transformer-bushing system. Koliou et al. (2013a, 2013b) demonstrated that the seismic performance of a transformer-bushing system could be improved by installing flexural stif- feners on the top cover plate of the transformer tank through numerical simulations and tests. Another measure to decrease the seismic responses of the bushing by increasing the turret stiffness was put forward and verified by Ma and Xie (2018). As to the seismic performance of the transformer bushing alone, Bellorini et al. (1998) numerically inves- tigated the amplification factors. Gilani et al. (1999a, 2001) made a seismic evaluation on two 230-kV bushings and retrofitted one of them to prevent oil leakage. It was observed through experimental studies on different transformer bushings that the bushings in lower voltage could survive high-intensity earthquakes (Gilani et al. 1998, 1999b; Whittaker et al. 2004, Fahad 2013).
Basic geometrical and physical parameters of typical porcelain transformer bushings of different voltages are compared in Table 1. The 1,100-kV UHV transformer bushing is taller, heavier, and more slender than its lower voltage counterparts, which makes it more vulner- able in earthquakes.
In previous researches, the seismic performance of an 1,100-kV UHV transformer bush- ing was investigated experimentally and numerically (Ma et al. 2018). Researches on the
seismic performance of the 1,100-kV UHV transformer bushing focused mainly on the seis- mic responses of the porcelain insulators rather than the metal flanges. In the UHV substa- tions in China, porcelain transformer bushings with cast-aluminum flanges are widely used. Considering the fractures of the metal flange in earthquakes in lower voltage bushings (Figure 1), some retrofitting countermeasures were considered on the flange to improve the seismic performance of the flange for utilizing in seismic areas. Therefore, the main pur- pose of this paper is to evaluate the seismic performance of the UHV transformer bushing widely used in Chinese non seismic areas and to verify whether the countermeasures taken on the flange could improve the seismic performance of the bushing using in seismic areas. The influence of different metal flanges on the seismic performance of the UHV transformer bushing was investigated. Two types of flanges were selected in this paper. The one made from cast aluminum with no seismic design is currently widely used in China. The other made from stainless steel was actually a retrofitted version of the first type. The FE and theoretical analyses were first carried out. Then the shaking table test was performed on two identical bushings using different flange types.
UHV BUSHING
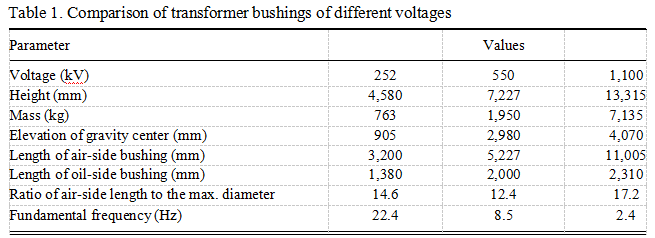
A typical 1,100-kV UHV transformer bushing with a total length of 13,315 mm is composed of two porcelain parts, one metal flange, four corona rings, and one dome (Figure 2). The 2,310-mm-long porcelain part is the oil-side bushing because it is always soaked in dielectric oil in the transformer tank. The 11,005-mm-long porcelain part outside the transformer tank is the air-side bushing, and the outside and inside diameters of the bottom cross section of it are 640 mm and 550 mm, respectively. The metal flange connects the two porcelain parts and fixes the UHV bushing on the transformer turret by bolts. Inside the hollow porcelain parts, there is a conductor with an aluminum core to transmit electric current. A 7-ton pretension is applied to the conductor, which makes the bushing under compression before external loads act on it. Other data about the bushing are listed in Table 2.
METAL FLANGES
Two types of metal flanges were studied in this paper, i.e., Flange-O and Flange-R, where the suffixes “O” and “R” mean the original and modified design, respectively. This naming rule was also applicable to the bushings. That is to say, Bushing-O and Bushing-R are the bushings with Flange-O and Flange-R, respectively. Most parameters of the two flanges were the same except for the following four aspects. First, Flange-O was made from cast alumi- num, a material widely used in high-voltage electrical equipment, and Flange-R was made from stainless steel, a material of very high strength and Young’s modulus. Second, the thick- nesses of the bottom plates were 34 mm and 36 mm in Flange-O and Flange-R, respectively (Figure 3). Third, there were 6 and 14 stiffeners in Flange-O and Flange-R, respectively (Figure 3). Finally, the stiffeners in Flange-R were extended to the outermost edge of the bottom plate (i.e., the stiffeners and the installation plate overlapped each other for
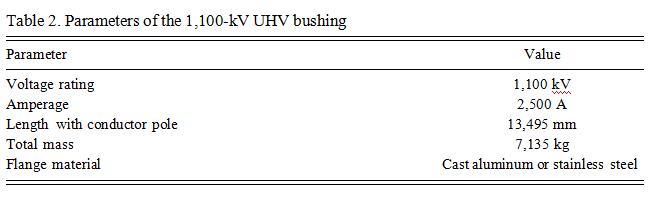
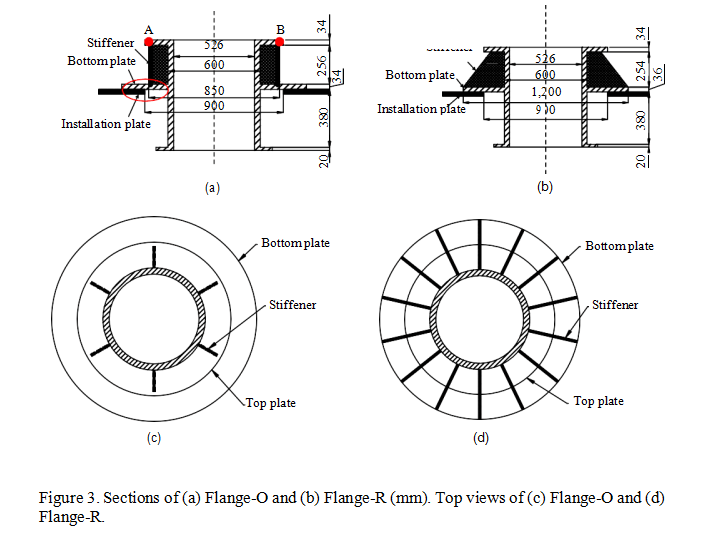


Figure 4. (a) Flange-O and (b) Flange-R mounted on the supporting frames with UHV bushings.
300 mm), but there existed a 50-mm gap between the stiffeners and the installation plate for Flange-O (Figure 3). Figure 4 shows the two flanges mounted on the supporting frames with UHV bushings.
FITITE ELEMENT METHOD AND THORETICAL ANALYSIS OF THE UHV BUSHINGS
FE ANALYSIS OF THE FLANGES
In order to analyze the seismic performance of the two types of flanges and to evaluate the flange influence on the seismic response of the UHV transformer bushing, two FE models of the 1,100-kV UHV porcelain transformer bushing with Flange-O and Flange-R, respectively, were established in ABAQUS (2010). In the shaking table test, to fix the bushings vertically on the table, a steel frame was fabricated and installed (the bottom part in Figure 4). The frame should be as stiff as possible to avoid its influence on the experimental results. The first frequency of the frame with the mass of the specimen should be larger than 33 Hz according to the stipulation in the Chinese standard (SCGG 2014). Before tests, the first frequency of the steel frame with the mass of the transformer bushing was calculated by FE analysis, and its value was 58 Hz, which indicated that the frame could be regarded as a rigid support. But the frame was still incorporated into the FE model to simulate the test results more accurately. The porcelain bushing, conductor, and metal flange were simulated by C3D8R solid ele- ments. The stiffeners, corona rings, and top installation plate of the supporting frame were simulated by S4R shell elements. In addition, B31 beam elements were used to simulate the other members in the supporting frame. The FE models had the same mass distribution and dimensions as the real bushing. Young’s modulus of 106 GPa was suggested by the manufacturer for the porcelain material. The FE model of the UHV bushing with Flange-O is shown in Figure 5a.
The results of modal analysis of the two bushings are shown in Figures 5 and 6, respec- tively. In the first mode shape of Bushing-O, the bushing itself experiences little deformation, and the large deflection at the bushing top is due mainly to the rocking effect of the flange
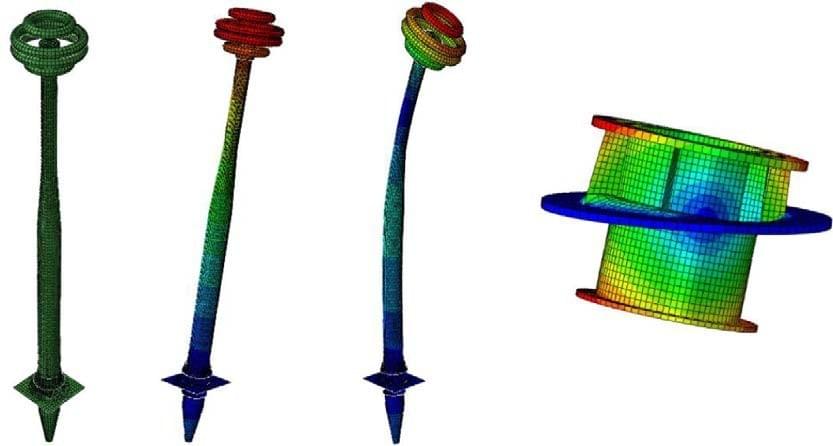
Figure 5. (a) FE model; (b) first mode shape of Bushing-O; (c) second mode shape of Bushing- O; and (d) deformation of Flange-O in the first mode shape.
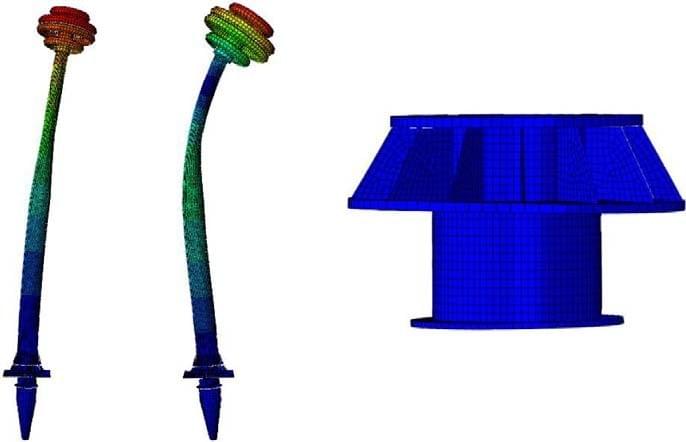
Figure 6. (a) First mode shape of Bushing-R (b) second mode shape of Bushing-R; and
(c) deformation of Flange-R in the first mode shape.
(Figure 5b). As shown in Figure 5d, the out-of-plane deformation of the flange bottom plate is significant. The first two mode shapes of Bushing-R are the bending deformation of the air- side bushing, as shown in Figure 6a and 6b. The deformation of Flange-R in the first mode shape is small compared with that of Flange-O, so the rocking effect of the flange is sup- pressed (Figure 6c). From the FE analysis, the first two frequencies of Bushing-O are
2.48 Hz and 15.62 Hz, respectively. The values of Bushing-R are 3.40 Hz and 17.92 Hz, respectively. The results indicate that the flange has great influence on the dynamic properties of the 1,100-kV UHV porcelain bushing. From the comparison of the resonance frequencies of the two bushings, it is obvious that Flange-R can greatly increase the stiffness of the UHV bushing.
EARTHQUAKE GROUND MOTION INPUT
To evaluate the seismic performance of the two UHV bushings, five artificial ground motion inputs based on the records selected from the PEER Ground Motion Database (PEER 2011) and modified by SeismoMatch software (2013) were adopted for the FE ana- lysis. According to the Chinese standard (SGCC 2014), the target peak ground acceleration (PGA) should be 0.3g. But to consider the amplification effects of the power transformer tanks and turrets, a dynamic amplification factor 2 was adopted, and thus the target PGA in the FE model was 0.6g. The spectra, the mean spectrum of the five earthquake ground motions, and the required response spectra (RRS) are shown in Figure 7a, and it was found that the mean spectrum could envelop the RRS well in the main frequencies region of the UHV transformer bushings. The time history of earthquake ground motion SGCC is recom- mended by the Chinese standard (SGCC 2014), and it was modified from the record of the Landers earthquake. The time history of earthquake ground motion SGCC is shown in Figure 7b, and the comparison of the acceleration response spectra (ARS) of this ground motion and the RRS in Chinese standard are presented in Figure 7c. According to the Chinese
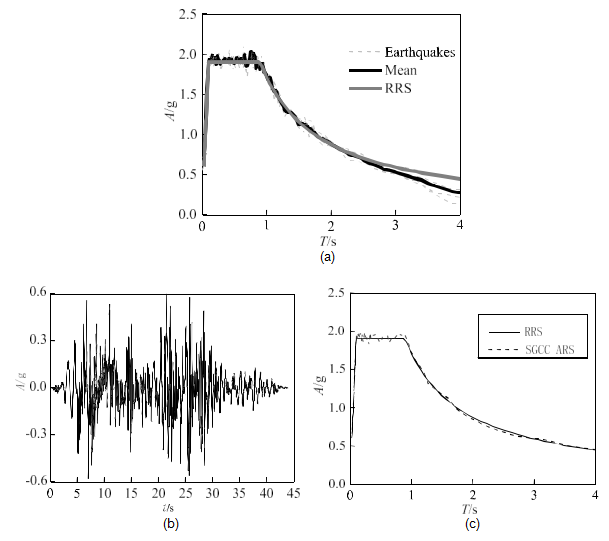
Figure 7. (a) Comparison of ARS and the mean ARS of the five earthquake ground motions;
acceleration time history of the SGCC ground motion; and (c) comparison of RRS and ARS of the SGCC ground motion (ξ = 2%).
standard, one earthquake ground motion of which the ARS could envelop the RRS in the standard should be adopted for the qualification test for evaluating the seismic performance of the UHV transformer bushing (SGCC 2014); the SGCC earthquake ground motion was also adopted in the shaking table tests for Bushing-O and Bushing-R.
STRESS RESPONSES OF THE FLANGES
As cast aluminum is a brittle material, the maximum principal stress of Flange-O was evaluated. Under the excitation of the SGCC earthquake ground motion, in the elastic ana- lysis, the maximum principal stress contours of the two flanges are shown in Figure 8. The maximum principal stress in Flange-O was 201.5 MPa, much larger than the tensile strength of cast aluminum, i.e., 130 MPa. Moreover, the maximum tensile stresses were located at the outermost intersection points of the stiffeners and the bottom plate, which meant that the
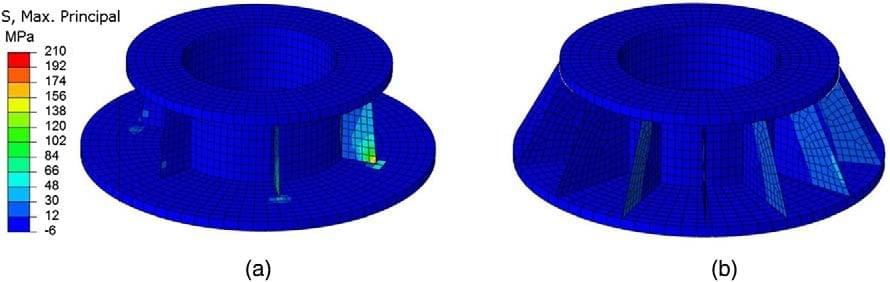
Figure 8. Maximum principal stress of (a) Flange-O and (b) Flange-R.
bottom plate and stiffeners would be damaged in earthquakes. Unfortunately, this was just the third failure type of high-voltage transformer bushings in the Wenchuan earthquake.
As seen in Figure 3a, the 50-mm gap between the stiffener edge and the installation plate made the direct load transfer from the air-side porcelain bushing to the supporting frame impossible. Punching shear forces were exerted on the flange bottom plate by the stiffeners. Because the contact area of the stiffener and the bottom plate was small, a very large stress would happen and fail the bottom plate.
For comparison with Flange-O, the maximum principal stress of Flange-R under the excitation of SGCC earthquake ground motions was computed, and the corresponding value was 32.3 MPa, much less than that in Flange-O. As stainless steel is a ductile mate- rial, the maximum von Mises stress of the Flange-R was adopted for evaluating the seismic performance of the flange, and the corresponding value was 34.1 MPa. According to the manufacturer, the yield strength of stainless steel is 205 MPa. The strength of the stainless material is much larger than maximum von Mises stress in the flange. Moreover, the max- imum stresses happened at the outer edges of the stiffeners. No failure would be expected from the analysis.
The maximum principal stresses at Flange-O and Flange-R under the excitation of the five earthquake ground motions are listed in Table 3. The maximum von Mises stress of Flange-R are also listed in Table 3. The maximum principal stresses of Flange-R are much
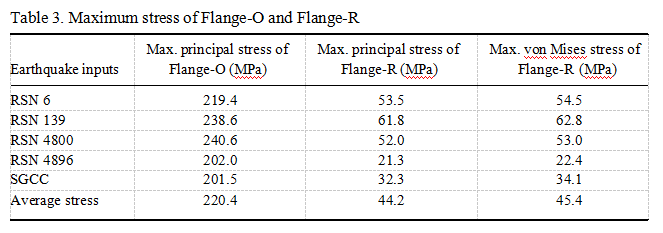
less than the corresponding value of Flange-O under the excitation of each earthquake ground motion. The average maximum principal stress of the cast aluminum is larger than the strength of this material, and the stainless steel flange meets the requirements of the standard, considering the average maximum von Mises stress is 45.4 MPa.
INFLUENCE OF THE FLANGE ON THE SEISMIC RESPONSES OF BUSHINGS
According to the above analysis, improper design of the stiffener could result in the failure of the flange, and subsequently influence the safety of the UHV transformer bushings. To evaluate the influence of the flange rocking effect on the seismic responses of the bushing, a theoretical model, shown in Figure 9a, was developed. The constraints by the supporting frame and the bottom plate of the flange were simplified as a horizontal spring and two vertical springs, respectively. The air-side bushing was equivalent to a cantilever beam. The horizontal displacements d at the top of the bushing could be decomposed into three components as:
d ¼ d1 þ d2 þ d3 (1)
where d1 was the translational displacement when the air-side bushing was seen as a rigid body. d2 was the rotational displacement generated by the rocking effect of the flange bottom plate, i.e., the bushing was assumed to be a rigid body and rotated around the bottom plate. d3 was the displacement generated by the deformation of the bushing itself. The diameter of
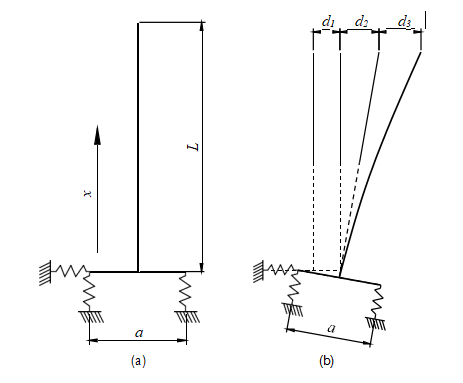
Figure 9. (a) Mechanical model and (b) displacement components of the UHV transformer bushing.
the flange top plate was a, and the displacements at the two end points of a diameter (points A and B in Figure 3a) in the vertical direction were represented by da and db. So the rotation angle θ at the base of the air-side bushing was:

(2)
Assuming the length of the air-side bushing was L, from Equations 1 and 2, the top displacements could be calculated as:
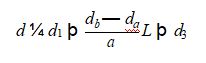
The acceleration at the bushing top could be derived by the second-order derivative of the displacement d versus time. After rearrangement, one got:
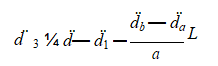
In Equation 4, d¨ , d¨ 1, d¨ a and d¨ b could be obtained from the FE analysis. So the accel-eration d¨ 2 ¼ db —da L at the bushing top generated by the rocking effect could be easily calculated and is shown in Figure 10, under the excitation of the SGCC earthquake ground motion, with a PGA of 0.6 g, in which d¨ 2 for Bushing-R is less than that for Bushing-O because the rocking effect of the bottom plate in Flange-R was suppressed.
The bending moment at the bottom cross section of the air-side bushing is a key para- meter for the UHV transformer bushing because the transformer bushing always cracked at this section in past earthquakes. The total bending moments M at this cross section could also
be decomposed into three components, i.e., Mt, Mr, and Mb corresponding to d¨ 1, d¨ 2, and d¨ 3,
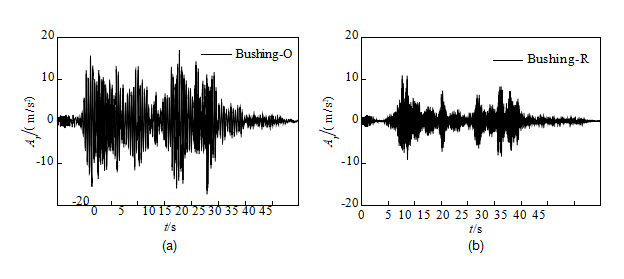
Figure 10. Acceleration at the bushing top generated by the rocking effect of the bottom plate for
(a) Bushing-O and (b) Bushing-R.
respectively. The total mass of the air-side bushing was m, and the mass distribution along the bushing was mðxÞ; one had
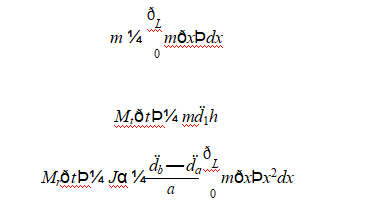
where h was the height of the gravity center of the air-side bushing, J was the rotational inertia, and α was the angular acceleration of the air-side bushing. In addition, the deflection d3 at any point of the air-side bushing was given by:
d3ðx,tÞ¼ ΦðxÞYðtÞ (7)
where Φ x was the mode shape matrix of the air-side bushing, which could be obtained from the FE model. Y t was the amplitude time history matrix for different mode shapes at the bushing top. From Equation 7:

The acceleration Abðx,tÞ generated by the deformation of the bushing was
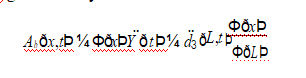
and the bending moments generated by the deformation was

Based on the FE results of the 0.6-g SGCC earthquake ground motion, the time histories of the bending moments given by Equations 5, 6, and 9 are shown in Figure 11. For Bushing- O, the bending moments generated by the translational accelerations are the smallest, while the bending moment generated by the rocking effect is the largest. The maximum value of it can take 74.1% of the peak total moment at the bottom cross section of the air-side bushing. When the peak total moment happens, the ratios of different components is
Mt∶Mr∶Mb 1∶3.73∶0.75, which indicates the rocking-effect-induced moment is dominant in the seismic responses of the transformer bushing. The bending moments for Bushing-R
generated by the rocking effect of Flange-R are shown in Figure 11d, which are obviously less than those for Bushing-O. This is because Flange-R effectively suppresses the rocking effect, and so decreases the corresponding bending moments.
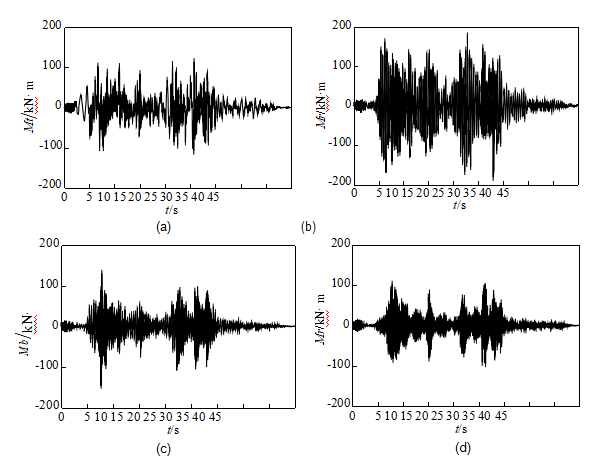
Figure 11. Bending moments generated by: (a) translational acceleration; (b) rocking effect of Flange-O; (c) bending deformation of Bushing-O; and (d) bending moment generated by the rocking effect of Flange-R.
SHAKING TABLE TESTS VERIFICATION
To verify the results of the FE and theoretical analyses, shaking table tests were carried out on two identical UHV transformer bushings using different flanges. The specimens and steel supporting frame were the same as those in the FE model. To facilitate the results com- parison, the target PGA and the SGCC earthquake ground motion used in the FE analysis were adopted.
TEST SCENARIO AND INSTRUMENTATION
According to the Chinese standard (SGCC 2014), the 1,100-kV UHV transformer bush- ing could be tested uniaxially for evaluating seismic performance. Table 4 summarizes the test scenarios for the two UHV bushings. White noise was used for identifying the dynamic characteristics of the two bushings before the tests and to check whether there was any struc- ture damage in the specimens after certain test scenarios. TS 2 was to optimize the table parameters and to minimize the tolerance between the table response spectra (TRS) and the RRS during the tests. TS 4 was to evaluate the seismic performance of the bushings and to verify the analysis results.

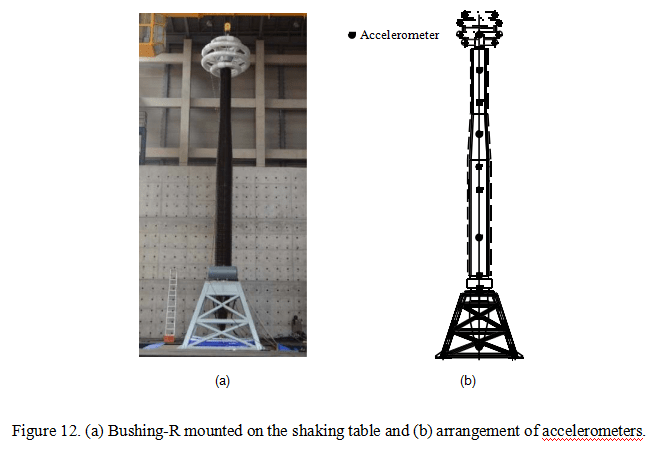
To obtain the dynamic properties and acceleration responses of the bushings, eight and ten accelerometers were arranged along the height of Bushing-O and Bushing-R, respec- tively. Since high-voltage electrical equipment always fractured at the bottom cross section in past earthquakes, two strain gauges were arranged at the bottom cross sections of the two air-side bushings along the vertical axis of the bushings in the main vibration direction to evaluate the strain in the porcelain. Bushing-R was mounted on the shaking table, and the arrangement of the accelerometers are shown in Figure 12.
DYNAMIC CHARACTERISTICS
According to the fundamental frequency of the steel frame, the frame is stiff enough. Transfer function of the UHV transformer bushing was obtained by the acceleration at the

top of the bushing with respect to the acceleration of the shaking table in the white noise input test. The frequencies of the two UHV bushings were obtained by the transfer func- tions. Table 5 presents the first two frequencies and damping ratios of the two bushings. Because the stainless steel Flange-R is of higher stiffness, the frequencies of Bushing-R are higher than those of Bushing-O, which is in accordance with the FE modal analysis. The damping ratios of 0.6% and 0.8% for Bushing-O and Bushing-R, respectively, were derived by the logarithmic decrement of the acceleration at the bushing tops. Both values are much less than the recommended one in the Chinese and IEEE standards (IEEE 2005, SGCC 2014).
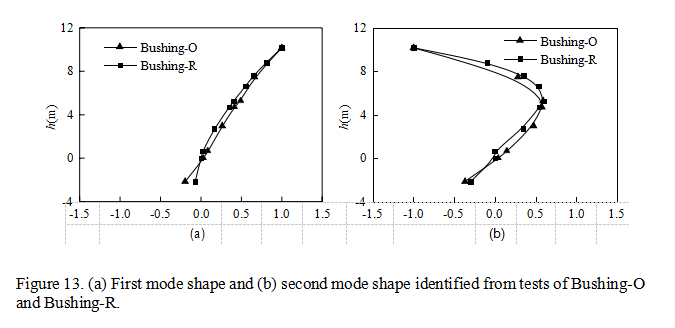
The first two mode shapes of Bushing-O and Bushing-R identified from the tests are shown in Figure 13. The height 0 in the vertical coordinates in Figure 13 means the top of the supporting frame. The first mode shape of Bushing-R is a bending shape. However, Bushing-O rotates around the flange obviously in its first mode, and the mode shape ampli- tudes are larger than the corresponding values of Bushing-R. The same conclusion could be drawn from the second mode shapes of the two bushings. Very close accordance of the first two resonance frequencies and mode shapes can be found between the FE analysis (listed in brackets in Table 5) and the tests, which validates the FE model in evaluating seismic per- formance of the UHV porcelain transformer bushings and the influence of different flanges. Using Flange-R to replace Flange-O, the stiffness of the UHV transformer bushing is increased, and the vibration modes are changed subsequently.
SEISMIC FAILURE OF FLANGE-O
In TS 4 for Bushing-O, at about 6–7 seconds after the seismic test had begun, discontin- uous fracturing sounds were heard. Meanwhile, oil leakage from the bottom plate of the cast- aluminum flange was observed. In order to maintain data integrity, the test continued. After the test, cracks along the intersection of the stiffeners and the bottom plate in Flange-O were found. Figure 14 shows the failure of Flange-O, which agrees well with the FE stress analysis (Figure 8a). Similar failures in 220-kV transformer bushings were observed in the Wenchuan earthquake, as shown in Figure 1, in which the flange bottom plates of three bushings all cracked. From the comparison of Figure 14 and Figure 1, it seems that the cast-aluminum flange should be retrofitted to improve its seismic performance. There was no visible damage in the porcelain bushing of Bushing-O after the tests. TS 5 was canceled for the failure of the specimen.
For Bushing-R, there was no visible damage in either the porcelain bushing or the stainless steel flange. Because the stiffeners of Flange-R were extended to the edge of the bottom plate, the load from the bushing could be directly transferred from the stiffeners to the supporting frame, which significantly reduced the shear stress and hence the tensile stress in the bottom plate.

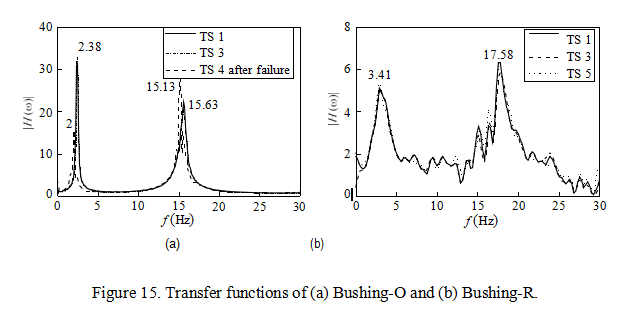
The transfer functions of TS 1 and TS 3 for Bushing-O are shown in Figure 15a. They are almost the same, which means there was no structure damage after TS 2. The transfer func- tions of the acceleration after the failure of Bushing-O in TS 4 are also shown in Figure 15a, which are much different from those of TS 1 and TS 3. The fundamental frequency of the bushing decreases from 2.4 Hz to 2 Hz, and the damping ratio increases from 0.6% to 1.1% because of the flange failure.
Bushing-R was tested with the same scenarios as Bushing-O. Figure 15b shows the trans- fer functions of TS 1, TS 3, and TS 5 of Bushing-R. All three curves are almost the same, which means that there was no structure damage in Bushing-R after test TS 2 and TS 4.
VERIFICATION OF THE FLANGE INFLUENCE
Define the bushing amplification factor (BAF) as the ratio of the peak acceleration at a point along the bushing height to the PGA. The BAFs of the two bushings in TS 4 are shown in Figure 16. It is obvious that the BAFs of Bushing-R are much smaller than those of
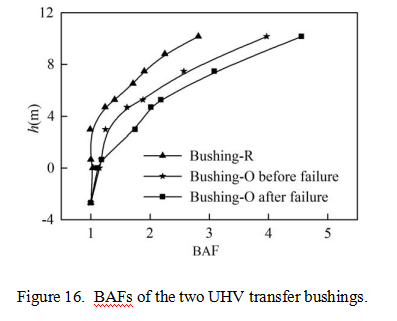
Bushing-O before and after failure. The retrofitted flange, i.e., Flange-R, increases the stiff- ness and the damping ratios of the transformer bushing and decreases the acceleration responses. It means that the metal flange has great influence on the dynamic characteristics of the bushing. Before the flange cracking, at the bottom part of the air-side bushing, the BAFs grow at a slower rate compared with those after the flange cracking. For Bushing- R, the increased stiffness of the flange leads to an even slower growing rate of the BAFs at the bottom part of the air-side bushing.
The maximum tensile strains obtained by the gauges of the two bushings were 145 με and 123 με. Considering the Young’s modulus of the porcelain material, the maximum seismic tensile stresses at the bottom cross section of the air-side bushing in Bushing-O and Bushing-R were 15.4 MPa and 13.1 MPa, respectively. The pretension of 7 tons in the conductor gen- erated a pre compressive stress in the porcelain bushing. According to the diameters of the bottom cross section, the pre compressive stress at this cross section is 0.8 MPa, which means that the maximum tensile stresses in Bushing-O and Bushing-R were 14.6 MPa and
12.3 MPa, respectively. Considering the ultimate strength of 40 MPa for the porcelain mate- rial, the porcelain insulators of the bushings were in a safety condition during the tests. This conclusion is in accordance with the phenomena observed in the tests. In addition, the max- imum stress in Bushing-R was less than that in Bushing-O due to the smaller seismic responses of Bushing-R.
The displacement at the top of high-voltage bushings is another key parameter to evaluate seismic performance of the bushings. On one hand, if the displacement is too large, tension will be introduced in the flexible bus connecting adjacent equipment and may destroy the electrical equipment (Mohammadi and Tehrani 2014). On the other hand, the position of the bushing top has influence on surrounding electromagnetic field, and the electrical clearance between different equipment is important for UHV equipment due to the high voltage. The displacement at the top of the two bushings was not measured directly because the bushings were too high to build a rigid frame for installing displacement meters. The values were calculated by quadratic integration from the accelerations recorded at the top of the air- side bushings using the method recommended by SeismoSignal software (Seismosoft 2018). The maximum displacements at the top of Bushing-O and Bushing-R are
170.5mm and 109.9 mm, respectively. As mentioned in the theoretical analysis, the rocking effect of the bottom plate of Flange-R is suppressed, and the frequencies of Bushing-R increased, which decreased the displacement of the bushing at the top.
Moreover, the displacement at the top of the oil-side bushing would affect the electro- magnetic field around the transformer tanks. The maximum displacements of the oil side bushing are 22.3 mm for Bushing-O and 3.6 mm for Bushing-R. The maximum displacement for Bushing-R is much less than that of Bushing-O. Since the dimensions and mass distribu- tion of the oil-side bushings are the same for the two specimens, it is the rocking effect of the flange that results in the difference. The rocking effect of Flange-R is suppressed and the high stiffness leads to a much smaller displacement.
From the shaking table test, it can be seen that Flange-R, having higher strength and stiffness than Flange-O, can effectively decreases the stress and displacement responses of the transformer bushing, so it is more suitable in seismic areas.
DISCUSSION
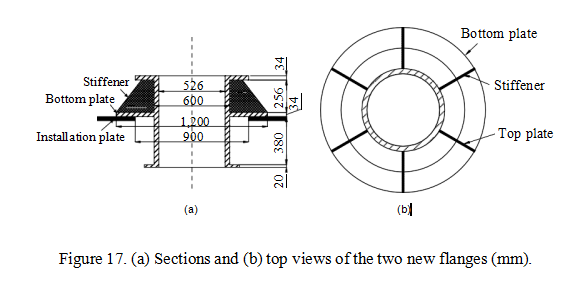
To improve seismic performance of the 1,100-kV UHV transformer bushing, the con- figurations of the stiffeners, the material, and the number of the stiffeners were changed in the flange. To investigate the influence of the material of the flange and the number of stiffeners on the stiffness and strength of the flange, the FE analyses on transformer bushings with two new flanges, named Flange-1 with six stiffeners made from cast aluminum and Flange-2 with six stiffeners made from stainless steel, were carried out. All the stiffeners have the same configuration as that of Flange-R and there is no gap between the stiffeners and the installa- tion plate. The other parameters of the two new flanges are the same as those of Flange-O. The configuration of the new flanges is shown in Figure 17.
The fundamental frequencies of the UHV transformer bushings increase in the sequence of with Flange-O, Flange-1, Flange-2, and Flange-R, listed in Table 6. Both the configuration and the material of the flange have influence on the fundamental frequency of the transformer bush- ing. After changing Flange-O to Flange-1, the fundamental frequency of the bushing increased by 20.3%. After changing cast aluminum to stainless steel (Flange-1 to Flange-2), a 10.1% fundamental frequency increase could be observed. Moreover, a 4.3% frequency increase was obtained by increasing the number of stiffeners from six to 14 (Flange-2 to Flange-R). The results indicate that the configuration of the stiffeners and the material of the flange play important roles in the dynamic properties of the transformer bushing.
The five earthquake ground motions were adopted in FE analyses of the transformer bushings with the four flanges. The maximum mean principal stresses of the four flanges and the maximum mean von Mises stress of the two stainless steel flanges are shown in Figure 18a. The maximum principal stresses happening from the largest to the smallest
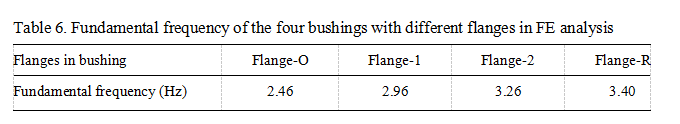
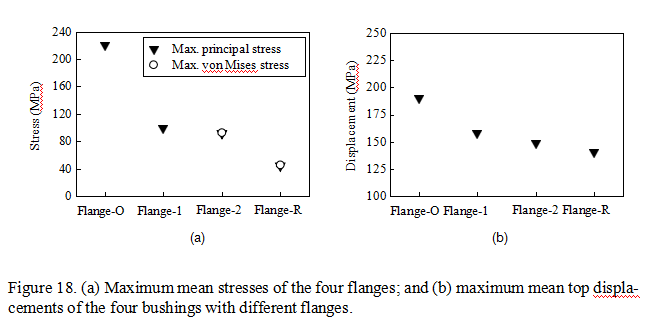
are in Flange-O, Flange-1, Flange-2, and Flange-R. The maximum principal stress in Flange- 1, cast aluminum for both the flange and six stiffeners, is less than the ultimate strength of cast aluminum, 130 MPa. In other words, after an appropriate design of the configuration of the stiffeners, even the cast aluminum can meet the seismic requirement for the UHV trans- former bushing. The maximum von Mises stress in Flange-2, stainless steel for both the flange and six stiffeners, is also less than the yield strength, 205 MPa, of stainless steel. The maximum mean principal stresses of Flange-1 and Flange-2 are similar, which means the configuration of stiffeners plays an important role in the seismic response of the flange. Due to the gap between the stiffener edge and the installation plate of the frame, there is no punching shear force in the interfaces of the stiffeners and the bottom plate, and it makes the flanges survive in earthquakes. With the number of stiffeners decreased from 14 to six, the contact area of the stiffener and the bottom plate reduces. It is the reason that the stress of Flange-R is less than that of the two new flanges.
The maximum mean top displacements of the bushings with the four different flanges are shown in Figure 18b. The top displacements decrease monotonically from bushing with Flange-O to Flange-R. After changing Flange-O to Flange-1, the out-of-plane deformation of the flange bottom plate was restrained by the stiffeners. Moreover, the out-of-plane stiff- ness of the bottom plate increased with changing the cast aluminum to stainless steel, a mate- rial with higher Young’s modulus. The two reasons increase the out-of-plane stiffness of the flange and decrease the top displacement of the transformer bushing.
The 1,100-kV UHV transformer bushings with different flanges have been tested and analyzed. However, there are several limitations in this paper, e.g., the bushings were tested and analyzed only uniaxially, and it is different with the inputs in real earthquakes; the dimen- sions and the mix proportion of the cement between the porcelain bushing and the metal flange may have influence on the stiffness and the seismic performance of the bushings, and it was ignored in this paper. Further works are needed on the three-dimensional excitation on the UHV transformer bushings, and the influence of the cement should be considered for evaluating seismic performance of the bushings.
The FE and theoretical analyses and shaking table tests were carried out on two identical 1,100-kV UHV transformer bushings with different flanges. The following conclusions can be obtained:
1.Flange-O has a lethal design deficiency, i.e., the force cannot be transferred from the top members to the support directly. The punching shear force applied by the stiffen- ers will fail the flange bottom plate. This is the main reason for the damages observed in the Wenchuan earthquake for high-voltage transformer bushings, since Flange-O is widely used in substations in China. Flange-R, a retrofitted ver- sion of Flange-O, has a more reasonable load-path than Flange-O, so the failure of the flange bottom plate can be avoided.
2.The rocking effect of the flange bottom plate is significant in the seismic responses of the UHV bushing. It not only dominates the bending moment at the bottom cross section of the air-side bushing, which may lead to the fracture of the porcelain bush- ing, but also influences the displacements at the tips of the bushings, which may violate the necessary electrical clearance between equipment.
3.The flanges of enough strength and stiffness can effectively suppress the rocking effect, so as to reduce the seismic responses of the flange and the UHV bushing. Since the proper design of the flange is so important, optimum flange type should be further developed.
ACKNOWLEDGMENTS
This study was financially supported by the Fok Ying Tung Education for Young Scientists from the Chinese Ministry of Education (Grant Number 114021) and Science and Technology Project of State Power Grid Cooperation of China (Grant Number SGTYHT/ 14-JS-188). The support is greatly appreciated.
REFERENCES
Bellorini, S., Salvetti, M., Bettinali, F., and Zafferani, G., 1998. Seismic qualification of trans- former high voltage bushings, IEEE Transactions on Power Delivery 13, 1208–1213.
Dassault Systemes Corporation, 2010. ABAQUS 6.10, software, available at https://www.3ds. com/products-services/simulia/products/abaqus/.
Eidinger, J., Davis, C., Tang, A., and Kempner, L., 2012. 9.0 M Tohoku Earthquake, March 11 2011, Performance of Water and Power Systems, G&E Engineering Systems, Oakland, CA. Fahad, M., 2013. Seismic evaluation and qualification of transformer bushings, Ph.D. Thesis,
State University of New York at Buffalo, Buffalo, NY.
Filiatrault, A., and Matt, H., 2005. Experimental seismic response of high-voltage transformer- bushing systems, Earthquake Spectra 21, 1009–1025.
Filiatrault, A., and Matt, H., 2006. Seismic response of high voltage electrical transformer– bushing systems, ASCE Journal of Structure Engineering 132, 287–295.
Fujisaki, E., Takhirov, S., Xie, Q., and Mosalam, K. M., 2014. Seismic vulnerability of power supply: Lessons Learned from recent earthquakes and future horizons of research, in Proceed- ings, 9th International Conference on Structural Dynamics (EURODYN 2014), European Association for Structural Dynamics, Volos, Greece, 345–350.
Gilani, A. S., Chavez, J. W., Fenves, G. L., and Whittaker, A. S., 1998. Seismic Evaluation of 196 kV Porcelain Transformer Bushings, Tech. Rep. PEER 1998/02, Pacific Earthquake Engi- neering Research Center, University of California, Berkeley, Berkeley, CA.
Gilani, A. S., Whittaker, A. S., and Fenves, G. L., 2001. Seismic evaluation and retrofit of 230-kV porcelain transformer bushings, Earthquake Spectra 17, 597–616.
Gilani, A. S., Whittaker, A. S., Fenves, G. L., and Fujisaki, E, 1999a. Seismic Evaluation and Retrofit of 230-kV Porcelain Transformer Bushings, Tech. Rep. PEER 1999/14, Pacific Earth- quake Engineering Research Center, University of California, Berkeley, Berkeley, CA.
Gilani, A. S., Whittaker, A. S., Fenves, G. L., and Fujisaki, E., 1999b. Seismic Evaluation of 550 kV Porcelain Transformer Bushings, Tech. Rep. PEER 1999/05, Pacific Earthquake Engineering Research Center, University of California, Berkeley, Berkeley, CA.
Goodno, B. J., Gould, N. C., Caldwell, P., and Gould, P., 2011. Effects of the January 2010 Hai- tian earthquake on selected electrical equipment, Earthquake Spectra 27, S251–S276.
Institute of Electrical and Electronics Engineers (IEEE), 2005. IEEE Recommended Practice for Seismic Design of Substations, IEEE Std 693-2005, New York, NY.
Johnson, F., and Iliev, K., 2012. Earthquake effects on SDG&E’s 500/230kV Imperial Valley Substation, in Proceedings, IEEE Power and Energy Society General Meeting, 22–26 July 2012, San Diego, CA.
Koliou, M., Filiatrault, A., and Reinhorn, A. M., 2013a. Seismic response of high-voltage trans- former-bushing systems incorporating flexural stiffeners I: Numerical study, Earthquake Spectra 29, 1335–1352.
Koliou, M., Filiatrault, A., and Reinhorn, A. M., 2013b. Seismic response of high-voltage trans- former-bushing systems incorporating flexural stiffeners II: Experimental study, Earthquake Spectra 29, 1353–1367.
Ma, G. -L., and Xie, Q., 2018. Dynamic interaction of high-voltage power transformer bushings, turrets, and tanks, Earthquake Spectra 34, 397–421.
Ma, G. -L., Xie, Q., and Whittaker, A. S., 2018. Physical and numerical simulations of the seismic response of a 1100 kV power transformer bushing, Earthquake Spectra, in press.
Mishima, T., Yokomura, T., and Takahashi, A., 2008. Lessons learned from the transformer fire in the Niigata-ken Chuetsu-oki earthquake and actions for solving the problems, Fire Disaster 58, 5–10 (in Japanese), available at https://ci.nii.ac.jp/naid/10021143851/.
Mohammadi, R. K., and Tehrani, A. P., 2014. An investigation on seismic behavior of three interconnected pieces of substation equipment, IEEE Transactions on Power Delivery 29, 1613–1620.
Pacific Earthquake Engineering Research Center (PEER), 2011. PEER Ground Motion Database, available at https://ngawest2.berkeley.edu/ (last accessed 12 December 2011).
Schiff, A. J., 1995. Northridge Earthquake: Lifeline Performance and Post-Rarthquake Response, Technical Council on Lifeline Earthquake Engineering, Monograph No. 8, Washington, DC.
Seismosoft, 2013. SeismoMatch v2.1, software, available at https://www.seismosoft.com/Public/ EditorUpload/Documen-ts/SeismoMatch.chm.
Seismosoft, 2018. SeismoSignal v2018, software, available at https://www.seismosoft.com/ Public/EditorU-pload/Documents/SeismoSignal.chm.
Shinozuka, M., Cheng, T. -C., Feng, M. Q., and Mau, S. -T., 1999. Seismic performance analysis of electric power systems, Research Progress and Accomplishments 1997–1999, University at Buffalo, State University of New York, Buffalo, NY, 61–69.
State Grid Corporation of China (SGCC), 2014. Technical Specification for Seismic Design of Ultra-High Voltage Porcelain Insulating Equipment and Installation/Maintenance to Energy Dissipation Devices, Q/GDW11132-2013, Beijing (in Chinese).
Whittaker, A. S., Fenves, G. L., and Gilani, A. S., 2004. Earthquake performance of porcelain transformer bushings, Earthquake Spectra 20, 205–223.
Xie, Q., and Zhu, R., 2011. Damage to electric power grid infrastructure caused by natural dis- asters in China, IEEE Power and Energy Magazine 9, 28–36.
(Received 25 December 2017; Accepted 6 July 2018)

